Нечеткое управление процессом вакуумной термической обработки
Вакуумная высокотемпературная установка «ПВ-1300» с нагревателями из композиционных материалов предназначена для термической обработки изделий из жаропрочных сплавов.
В состав двухкамерной установки входят: камера нагрева с теплоизоляцией из углеродных материалов; камера охлаждения с теплообменником и охлаждающим вентилятором; пневматический технологический затвор, разделяющий камеры; устройство для подъёма и опускания садки; узел для перемещения садки; тележка для перемещения теплообменника; вакуумная и пневматическая системы; система водяного охлаждения; система подачи инертного газа; система управления.
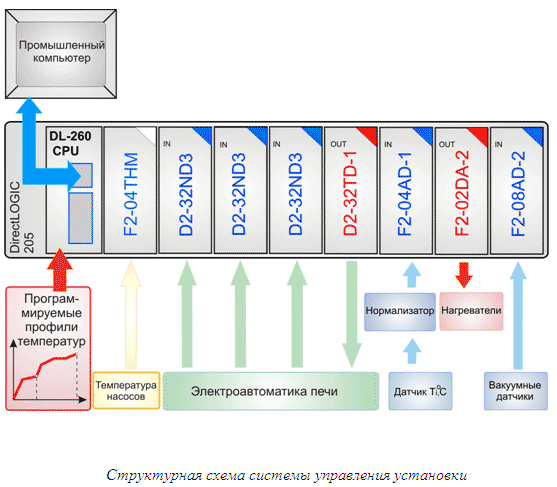
Управление работой системы на нижнем уровне производится от сертифицированного контроллера типа PLC Direct Logic DL-205, на верхнем уровне - компьютера промышленного исполнения с сенсорным экраном.
СУ обеспечивает работу печи в следующих режимах: «Ручное управление», «Программирование» и «Автоматизированный».
В режиме «Ручное управление» обеспечивается управление системами установки (вакуумной, нагрева) с пульта управления для доведения цикла термической обработки в случае сбоя автоматизированного режима.
В режиме «Программирование» можно ввести значения технологических параметров, обеспечивающих процесс термической обработки: программу термообработки (количество участков, температура, скорость нагрева и время обработки), допустимый диапазон рабочего вакуума.
В режиме «Автоматизированный» обеспечена реализация макрокоманд процесса термической обработки.
Для обеспечения безопасной работы установки и обслуживающего персонала, предотвращения неправильных действий оператора выполнены необходимые блокировки по вакууму и охлаждению.
При управлении технологическим процессом термической обработки изделий из жаропрочных сплавов с нагревателями из композиционных материалов традиционно используются классические П, ПИ и ПИД-регуляторы. Оптимальная настройка их коэффициентов, проверка алгоритмов на объекте представляет собой достаточно сложную задачу. В то же время опытный оператор достаточно уверенно справляется с решением этой задачи, используя показание текущей температуры и её первой производной. Данный процесс характеризуется достаточно большой инерционностью (время вычислительного цикла может достигать 30 секунд).
Во время проведения пуско-наладочных работ по вводу в эксплуатацию вакуумной печи типа «ПВ-1300» было применено управление на базе эвристических алгоритмов с использованием языка нечеткой логики. Простота алгоритма, основанного на опыте и интуиции оператора-термиста, позволила существенно сократить время настройки регулятора температуры.
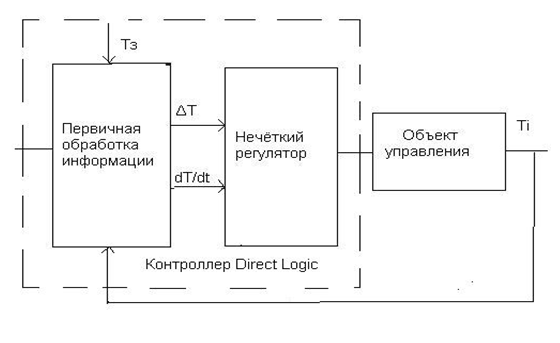
Рассмотрим пример нечеткого управления вакуумной печи нагрева с нагревателями из композиционных углеродных материалов. Нечёткий регулятор функционирует в прямом контуре.
Функции нечеткого регулятора выполняет программный модуль контроллера Direct Logic 205, который рассчитывает разницу между текущей и заданной температурой, первую производную изменения температуры.
|
Рис. 2. Нечеткая система регулирования температуры в прямом контуре управления |
Задача управления состоит в определении значения управляющего сигнала на цифроаналоговый преобразователь контроллера по следующим входным переменным: ΔT (разница между текущей и заданной температурой), dT/dt (первая производная изменения температуры за время вычислительного цикла).
Для формализации знаний оператора рассмотрим несколько случаев:
1. ΔT – большая положительная, dT/dt – положительная, тогда уставка на ЦАП – минимальная.
2. ΔT – большая положительная, dT/dt – отрицательная, тогда уставка на ЦАП – малая.
3. ΔT – большая положительная, dT/dt – малая, тогда уставка на ЦАП – минимальная.
4. ΔT – средняя положительная, dT/dt – положительная, тогда уставка на ЦАП – малая.
5. ΔT – средняя положительная, dT/dt – отрицательная, тогда уставка на ЦАП – средняя.
6. ΔT – средняя положительная, dT/dt – малая, тогда уставка на ЦАП – средняя.
7. ΔT – малая положительная, dT/dt – положительная, тогда уставка на ЦАП – средняя.
8. ΔT – малая положительная, dT/dt – отрицательная, тогда уставка на ЦАП – большая.
9. ΔT – малая положительная, dT/dt – малая, тогда уставка на ЦАП – средняя.
10. ΔT – нулевая, dT/dt – положительная, тогда уставка на ЦАП – малая.
11. ΔT – нулевая, dT/dt – отрицательная, тогда уставка на ЦАП – большая.
12. ΔT – нулевая, dT/dt – малая, тогда уставка на ЦАП – средняя.
13. ΔT – малая отрицательная, dT/dt – положительная, тогда уставка на ЦАП – средняя.
14. ΔT – малая отрицательная, dT/dt – отрицательная, тогда уставка на ЦАП – большая.
15. ΔT – малая отрицательная, dT/dt – малая, тогда уставка на ЦАП – большая.
16. ΔT – средняя отрицательная, dT/dt – положительная, тогда уставка на ЦАП – большая.
17. ΔT – средняя отрицательная, dT/dt – отрицательная, тогда уставка на ЦАП – максимальная.
18. ΔT – средняя отрицательная, dT/dt – малая, тогда уставка на ЦАП – большая.
19. ΔT – большая отрицательная, dT/dt – положительная, тогда уставка на ЦАП – большая.
20. ΔT – большая отрицательная, dT/dt – отрицательная, тогда уставка на ЦАП – максимальная.
21. ΔT – большая отрицательная, dT/dt – малая, тогда уставка на ЦАП – максимальная.
Общий логический вывод осуществляется за следующие 4 этапа: нечеткость (введение нечеткости, фазификация); логический вывод - вычисленное значение истинности для предпосылок каждого правила применяется к заключениям каждого правила; композиция - все нечеткие подмножества во всех правилах объединяются вместе, чтобы формировать одно нечёткое подмножество для каждой переменной вывода; приведение к четкости (дефазификация).
Итак, на первом этапе необходимо определить степени для предпосылок каждого правила: Аi(ΔТ), Bi(dТ/dt).
Далее находятся уровни «отсечения» для предпосылок каждого из правил с использованием операции минимум:
ά i = min(Аi(ΔТ), Bi(dТ/dt))
Определяем значение переменной вывода по формуле:
Z = ∑ ά i z i/ ∑ ά i
Входной сигнал от термопары через нормализатор поступает на аналого-цифровой модуль «F2-04AD-1» контроллера. Предположим, что аналоговый сигнал ограничен диапазоном [↔1, 1] и преобразуется в цифровую форму с дискретностью 0,2: -1; -0,8; -0,6; -0,4; -0,2; 0; 0,2; 0,4; 0,6; 0,8; 1.
Определим для нечеткой лингвистической переменной ΔT нечеткие множества с соответствующей функцией принадлежности:
А1 – большая положительная;
А2 – средняя положительная;
А3 – малая положительная;
А4 – нулевая;
А5 – малая отрицательная;
А6 – средняя отрицательная;
А7 – большая отрицательная.
Таблица 1. Значения функций принадлежности лингвистической переменной ΔT
|
АЦП ºС |
-1 (-10) |
-0,8 (-8) |
-0,6 (-6) |
-0,4 (-4) |
-0,2 (-2) |
0 0 |
0,2 (2) |
0,4 (4) |
0,6 (6) |
0,8 (8) |
1 (10) |
|
А1(ΔТ) |
0 |
0 |
0 |
0 |
0 |
0 |
0,2 |
0,4 |
0,6 |
0,8 |
1 |
|
А2(ΔТ) |
0 |
0 |
0 |
0 |
0 |
0,2 |
0,4 |
0,8 |
1 |
0,8 |
0,6 |
|
А3(ΔТ) |
0 |
0 |
0 |
0 |
0 |
0,5 |
1 |
0,5 |
0 |
0 |
0 |
|
А4(ΔТ) |
0 |
0 |
0 |
0,2 |
0,4 |
1 |
0,4 |
0,2 |
0 |
0 |
0 |
|
А5(ΔТ) |
0 |
0 |
0 |
0,5 |
1 |
0,5 |
0 |
0 |
0 |
0 |
0 |
|
А6(ΔТ) |
0,6 |
0,8 |
1 |
0,8 |
0,4 |
0,2 |
0 |
0 |
0 |
0 |
0 |
|
А7(ΔТ) |
1 |
0,8 |
0,6 |
0,4 |
0,2 |
0 |
0 |
0 |
0 |
0 |
0 |
Определим для нечеткой лингвистической переменной dT/dt нечеткие множества с соответствующей функцией принадлежности:
B1 – положительная;
B2 – малая;
B3 – отрицательная.
Таблица 2. Значения функций принадлежности лингвистической переменной dT/dt
|
АЦП ºС/цикл |
-1 -2,5 |
-0,8 -2 |
-0,6 -1,5 |
-0,4 -1 |
-0,2 -0,5 |
0 0 |
0,2 0,5 |
0,4 1 |
0,6 1,5 |
0,8 2 |
1 2,5 |
|
B1(dТ/dt) |
0 |
0 |
0 |
0 |
0 |
0,2 |
0,5 |
1 |
0,8 |
0,6 |
0,4 |
|
B2(dТ/dt) |
0 |
0 |
0,3 |
0,5 |
0,8 |
1 |
0,8 |
0,5 |
0,3 |
0 |
0 |
|
B3(dТ/dt) |
0,4 |
0,6 |
0,8 |
1 |
0.6 |
0,3 |
1 |
0,5 |
0 |
0 |
0 |
Выходной сигнал формируется с помощью ЦАП и имеет 5 уровней: -1 (минимальный), -0,5 (малый), 0 (средний), 0,5 (большой), 1 (максимальный). Управляющий аналоговый сигнал (0 … 10 В) записывается в ячейку модуля аналогового выхода F2-02DA-2.
Определим для нечетких лингвистических переменных ΔT, dT/dt нечеткие множества с соответствующими идентификаторами для функций принадлежности μ(ΔТ), μ(dT/dt).
Для μ(ΔТ) эти идентификаторы имеют вид:
РМ – отклонение положительное большое (более +5);
PS - отклонение положительное среднее (более +3);
PSZ - отклонение положительное малое (более +1);
ZR - отклонение нулевое (менее 1);
NSZ - отклонение отрицательное малое (более -1);
NS - отклонение отрицательное среднее (более -3);
NM - отклонение отрицательное большое (более -5).
С учетом заданных нечетких множеств база правил эвристического алгоритма имеет вид:
R1: если ΔT= РМ, dT/dt= РS, тогда УПР=↔1
R2: если ΔT= PM, dT/dt= NS, тогда УПР=↔0,5
R3: если ΔT= PM, dT/dt= ZR, тогда УПР=↔1
R4: если ΔT= РS, dT/dt= РS, тогда УПР=↔0,5
R5: если ΔT= PS, dT/dt= NS, тогда УПР=0
R6: если ΔT= PS, dT/dt= ZR, тогда УПР=0
R7: если ΔT= РSZ, dT/dt= РS, тогда УПР=0
R8: если ΔT= PSZ, dT/dt= NS, тогда УПР=0,5
R9: если ΔT= PSZ, dT/dt= ZR, тогда УПР=0
R10: если ΔT= ZR, dT/dt= РS, тогда УПР=↔0,5
R11: если ΔT= ZR, dT/dt= NS, тогда УПР=0,5
R12: если ΔT= ZR, dT/dt= ZR, тогда УПР=0
R13: если ΔT= NSZ, dT/dt= РS, тогда УПР=0
R14: если ΔT= NSZ, dT/dt= NS, тогда УПР=0,5
R15: если ΔT= NSZ, dT/dt= ZR, тогда УПР=0,5
R16: если ΔT= NS, dT/dt= РS, тогда УПР=0,5
R17: если ΔT= NS, dT/dt= NS, тогда УПР=1
R18: если ΔT= NS, dT/dt= ZR, тогда УПР=0,5
R19: если ΔT= NM, dT/dt= РS, тогда УПР=0,5
R20: если ΔT= NM, dT/dt= NS, тогда УПР=1
R21: если ΔT= NM, dT/dt= ZR, тогда УПР=1
Рассмотрим конкретный вариант выбора решения при следующих значениях входных переменных: ΔT = 4ºC, dT/dt = -1ºC/цикл.
ά1 = min(0,4; 0) = 0 и z = ↔1
ά2 = min(0,4; 0,5) = 0,4 и z = ↔0,5
ά3 = min(0,4; 1) = 0,4 и z = ↔1
ά4 = min(0,8; 0) = 0 и z = ↔0,5
ά5 = min(0,8; 0,5) = 0,5 и z = 0
ά6 = min(0,8; 1) = 0,8 и z = 0
ά7 = min(0,5; 0) = 0 и z = 0
ά8 = min(0,5; 0,5) = 0,5 и z = 0,5
ά9 = min(0,5; 1) = 0,5 и z = 0
ά10 = min(0,2; 0) = 0 и z = ↔0,5
ά11 = min(0,2; 0,5) = 0,2 и z = 0,5
ά12 = min(0,2; 1) = 0,2 и z = 0
ά13 = min(0; 0) = 0 и z = 0
ά14 = min(0; 0,5) = 0 и z = 0,5
ά15 = min(0; 1) = 0 и z = 0,5
ά16 = min(0; 0) = 0 и z = 0,5
ά17 = min(0; 0,5) = 0 и z = 1
ά18 = min(0; 1) = 0 и z = 0,5
ά19 = min(0; 0) = 0 и z = 0,5
ά20 = min(0; 0,5) = 0 и z = 1
ά21 = min(0; 1) = 0 и z = 1
Выход регулятора:
Z = (0 ↔1 + 0,4 ↔0,5 + 0,4 ↔1 + 0,8 ↔0,5 + 0,5 0 + 0,8 0 + 0 0 + 0,5 0,5 + 0,5 0 + 0 ↔0,5 + 0,2 0,5 + 0,2 0 + 0 0 + 0 0,5 + 0 0,5 + 0 0,5 + 0 1 + 0 0,5 + 0 0,5 + 0 1 + 0 1)/(0 + 0,4 + 0,4 + 0 + 0,5 + 0,8 + 0 + 0,5 + 0,5 + 0 + 0,2 + 0,2 + 0 + 0 + 0 + 0 + 0 + 0 + 0 + 0 + 0) = 0,1
Выход регулятора соответствует z = 0 (средняя).
Аналогично значение выходного сигнала регулятора z рассчитываются при других значениях ΔT и dT/dt.
Реализация данного алгоритма в виде нечеткого контроллера в прямом контуре управления позволяет исключить оператора и передать его функции нечеткой системе регулирования.
Приведенный пример показывает преимущество нечеткой системы регулирования по сравнению с традиционной системой регулирования простотой своей технической реализации.